🌳 Understanding Binary Search Trees (BST) 🌳
What is a Binary Search Tree?

In the world of computer science a tree looks like this! 😆
If you are given a list of numbers like [2, 8, 12, 17, 22, 29, 32] and suppose you need to find the closest number to a given target value, then you can use a BST.
off course you know BST is a Data Structure & Binary means “two things”. How does it look on paper?
17
/ \
8 29
/ \ / \
2 12 22 32
Looks like a Pyramid, right? then why everyone is calling it a Tree? may be due to the branches. idk! 🤷♂️
the same tree can also be represented as below
2
\
8
\
12
\
17
\
22
\
29
\
32
looks like a Staircase! Geniuses are saying that this is also a tree!
Now you may be thinking, why do we need to represent data in a BST? We have linked list, right?
You are correct. If the input data is already sorted, using a Binary Search Tree (BST) might not be the best choice in terms of efficiency and balance. This is because a sorted input can lead to the creation of a degenerate BST, which essentially becomes a linked list.
For fun, I entered the input in a random order, so that we don’t get a Staircase!
BST has some advantages, lets explore.
Game Rules:
-
17 is called the root.
-
Left Subtree are always smaller than the value of the parent node, while the values in the Right Subtree are always larger.
-
To insert a new value into the BST, you start at the root and compare the value with the current node. If the value is smaller, you go to the left subtree; if it’s larger, you go to the right subtree, and you keep doing this until you find an empty spot (a null branch) where you can place the new value.
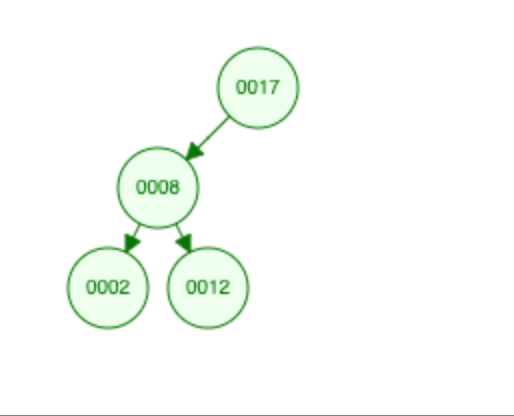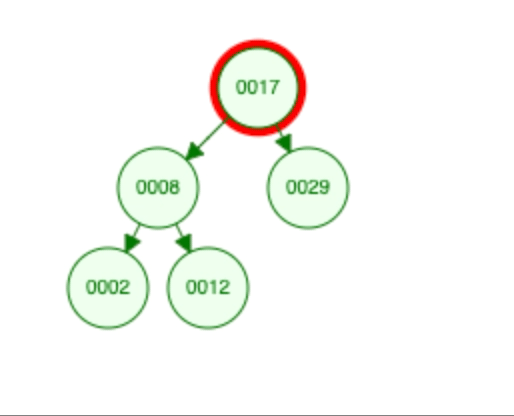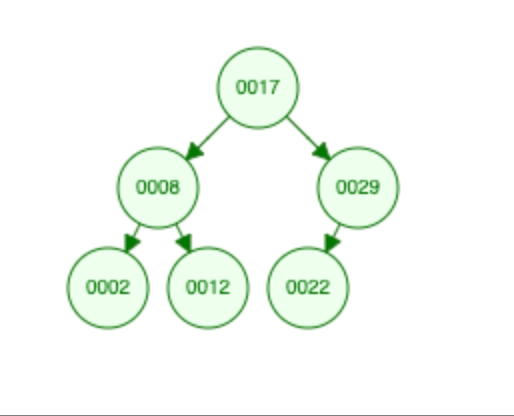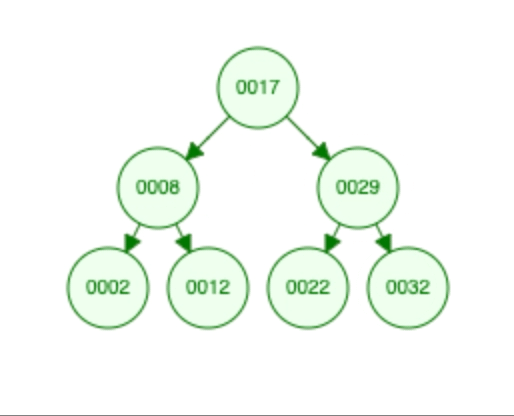
- To find a value in the BST, you start at the root and compare the value with the current node. If the value matches, you found it! If it’s smaller, you go to the left subtree; if it’s larger, you go to the right subtree. You keep doing this until you find the value or reach a dead end (a null branch), which means the value is not in the tree. eg : finding 12 will be like.

- To delete a value from the BST, you first find the node with that value. Then, you have three cases to consider: the node has no children, it has one child, or it has two children. Depending on the case, you rearrange the tree to maintain the BST property.
Now lets play with BST!
Our task is to find the closest number to a given target value. Target = 20, for fun, lets take the following “Treeee” 😆
17
/ \
8 29
/ \ / \
2 12 22 32
-
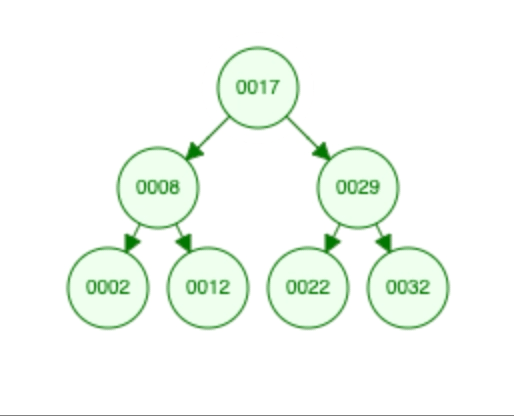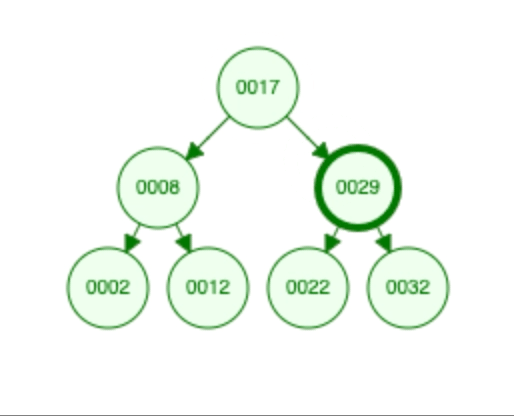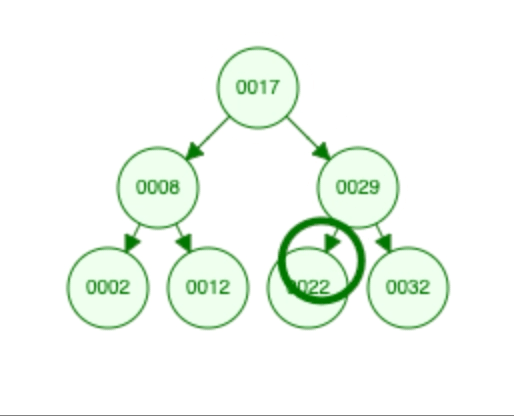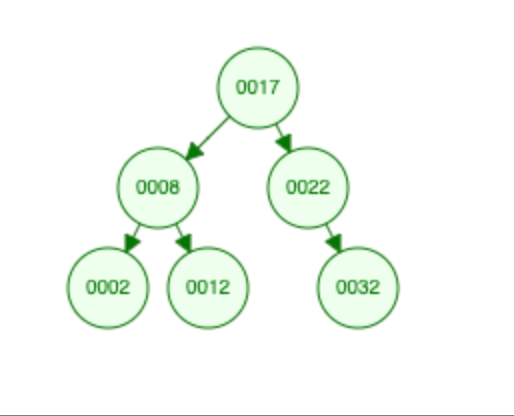
Perform a Binary Search: Start at the root of the BST and perform a binary search to find the closest number to the target (20). Traverse the BST based on the target value and compare the current node’s value to the target value.
-
Current node value = 17
-
Target (20) is greater than 17, move to the right subtree.
-
Current node value = 29
-
Target (20) is less than 29, move to the left subtree.
-
Current node value = 22
-
Target (20) is less than 22, move to the left subtree which is null.

The traversal leads us to the node with the value 22, which is the closest number to the target value 20 in the list.
The BST efficiently narrows down the search space through its binary search property, allowing us to find the closest number to the target in O(log n) time, where n is the number of nodes in the BST.
This example demonstrates how a BST can be beneficial for certain search-related problems.
Here are a couple of areas where binary search trees may be relevant:
-
Autocomplete and Search Suggestions
-
Caching: Binary search trees can be used in caching mechanisms to store frequently accessed data for faster retrieval.
-
Spell Checking
-
Address Book Applications
-
Stock Market Analysis: In stock market analysis and financial trading, binary search trees can be used to store and search historical stock price data based on time or date.
-
Geographic Information Systems (GIS)
-
Memory Management: In certain memory management techniques, like buddy allocation, binary search trees can be used to efficiently track free memory blocks of different sizes, facilitating memory allocation and deallocation.
-
Dictionary Implementations
-
Symbol Tables: In compilers, interpreters, and other language processing tools
-
File Systems: File systems on computers often use binary search trees to store file and directory information.
Congratulations 🎉 , now you know what is a Binary Search Tree is.
One Moment : Thank you for taking the time to read my blog. I hope you found it helpful, insightful, or even entertaining. If it made a positive impact on your day or provided you with valuable information, I’d be thrilled to know!
If you enjoyed the content and would like to show your appreciation, you can support me in two ways:
-
Give it a Clap: Just click on the 👏 button at the end of the article. Each clap is a virtual pat on the back and a way to let me know that you liked the blog.
-
Buy Me a Coffee: If you’re feeling extra generous and would like to support my work further. To leave a tip, simply click on the “Tip” button, and any amount you’re comfortable with is greatly appreciated. Your contribution will keep me fueled and motivated to create more content in the future.
Your support means a lot to me, and it encourages me to continue sharing my knowledge and experiences. I’m grateful for each and every reader who finds value in what I write. 🙏
❤️ Feeling the love? Give me a tip on Medium!